伪随机数采样
假设计算机能够生成服从于[0,1] 均匀分布的随机变量/随机数(random numbers/variables, r.v.'s),那么所谓生成随机样本(generating random sample)的任务就是根据上述假设寻找一个快速的生成其他非均匀分布的随机变量(non-uniform r.v.'s)的方法。该任务也被称之为采样或伪随机数采样(pseudo-random number sampling)。
逆变换采样方法
逆变换采样(inverse transform sampling)是一种给定想要生成的随机变量X 的累计分布函数(Cumulative Distribution Function, CDF)FX 后,通过对其进行逆变换(反函数)实现随机样本生成的方法。其中FX 是一个连续且严格单调递增的函数。
具体来说,我们需要找到一个变换/映射T:[0,1]↦R 使得U∼Unif[0,1] 变换为服从FX 的新随机变量X,即T(U)=X。不难发现,有:
FX(x)=Pr(X≤x)=Pr(T(U)≤x)=Pr(U≤T−1(x))=T−1(x)
也就是说,根据任意一个随机数u∈[0,1] ,我们可以生成另一个随机数x=T(u)=FX−1(u),其中FX−1(u):=inf{x∣FX(x)≥u},inf 表示 infimum,即下确界。这么定义该反函数的原因是 CDF 是单调且右连续的。
Example #1
指数分布
标准拉普拉斯分布
逆变换采样网格法
对于X∈R 的随机变量X∼FX(x),设其 support 为SX ,即所有可能的取值的集合。为了生成X,我们可以选择适当的网格{xi}i=1d 将SX 覆盖。
则X 的概率密度函数(Probability Density Function, PDF)可以使用离散随机变量{xi}i=1d 的离散概率分布进行近似:
pi=∑j=1dfX(xj)fX(xi)i=1,2,...,d
进而采用离散分布的 CDF 使用 inverse sampling 生成。
显然,The Grid Method 同样可以适用于一些非标准的分布函数,乃至部分很难求“反”的函数。
Example #2
截断正态分布
【文献阅读 02】截断(truncated)正态分布 - 知乎 (zhihu.com)
接受-拒绝采样方法
Inverse CDF 采样方法固然有效,但对于那些 CDF 很难通过对 PDF 的积分得到,或者 CDF 的反函数不容易求得的分布,我们可能需要用到另外一种采样方法。而接受-拒绝采样方法(Acceptance-Rejection sampling),通常也直接称为拒绝采样(Rejection sampling)就是一种可以解决上述问题的方法之一。
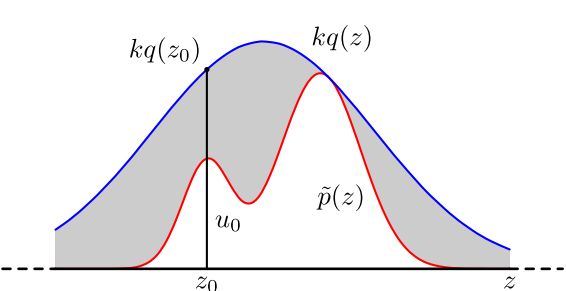
参考上图,假设p(x) 是目标采样分布X∼p(⋅) 的 PDF,它在自身的支撑集SX 内可以被另一个 PDF 为q(x) 的分布Y∼q(⋅) 包络起来(Y 的分布称为 提议分布 proposal distribution)。即:
p(x)≤k⋅q(x)∀x∈SX
其中k≥1 为包络常数(envelope constant),q(x) 是提议分布的 PDF,也称为包络密度函数(envelope density)。
Rejection sampling 的算法步骤如下:
- 独立地生成两个随机变量U∼U[0,1] 和Y∼q(⋅);
- 如果U≤p(Y)/kq(Y) 则Y 即为所要的服从于p(⋅) 的随机变量,接受Y,返回X=Y;否则拒绝Y 并返回到第一步。
感性认知
从图像上来理解,p(z0)/kq(z0) 越趋近于1,说明此时p(z0) 和kq(z0) 的距离越小,图中竖直线段上处于灰色阴影部分的线段长度就越短,此时在线段上进行均匀采样,就有极大的概率使采样点u0 落在非阴影区域,以该概率判断是接受还是拒绝z0 。
显然 rejection sampling 是符合直觉的认知策略,下面还将在理论上进行推导验证该方法的可行性。
理论证明
令h(Y)=p(Y)/kq(Y) ,从而:
h(x)⋅q(x)=k1⋅p(x)
根据贝叶斯定理,有:
fY(x∣U≤h(Y))=Pr{U≤h(Y)}Pr{U≤h(Y)∣Y=x}⋅q(x)=Pr{U≤h(Y)}Pr{U≤h(x)}⋅q(x)=Pr{U≤h(Y)}h(x)⋅q(x)
而分母:
Pr{U≤h(Y)}=∫SXPr{U≤h(Y)∣Y=x}⋅q(x)dx=∫SXh(x)⋅q(x)dx=k1∫SXp(x)dx=k1
综上可得,fY(x∣U≤h(Y))=p(x)。
也就是说,在U≤h(Y) 的条件下,如果一个随机变量x 服从于fY(⋅)=q(⋅) ,那么它也服从于p(⋅)。
算法有效性
从图像上来看,过大的k 值会让kq(x) 的图像远在p(x) 上方,阴影部分最多,拒绝的概率也就增大了。此外根据前面的推导我们知道,Pr{U≤h(Y)}=1/k。也就是说我们随机生成的能满足接受条件的随机变量的有效性与包络常数k 成反比。
更数学化地,令算法迭代次数为N ,则获得一次被接受的随机数对(U,X) 的迭代数n 同样是一个随机变量,它服从于几何分布:
Pr{N=n}=p(1−p)n−1,n≥1
其中,p=Pr{U≤h(Y)}=1/k.
该几何分布的期望E(N)=1/p=k,表明算法第一次获得被接受的随机数时的迭代次数的期望。
总而言之,k 尽可能地小,算法的迭代次数就能尽可能地少,每次迭代生成的随机变量就尽可能多地符合条件并被接受。由p(x)≤k⋅q(x) 可推出一个最优的k 应该满足:
k=x∈SXmaxq(x)p(x)
实际上,在实践中往往需要同时选取一个合适的包络函数,即从一个函数族{qθ(x):θ∈Θ} 中选择 candidate envelopes。所以我们一般是对所有的θ 都找到一个两个分布距离最远的坐标x^θ:
x^θ=argx∈SXmaxqθ(x)p(x)=argx∈SXmax[logp(x)−logqθ(x)]
然后从中寻得最小的k:
k=θ∈Θminkθ=θ∈Θminqθ(x^)p(x^)
Example #3
对数凹密度函数
截断正态分布
数值积分
拉普拉斯近似
虽然前面提到的采样方法已经能够应对非标准的分布,但是寻找合适的建议分布(包络函数)是较为困难的。此外,在我们对后验概率分布(posterior distribution)等这种概率密度难以给出解析式的分布感兴趣时,如何对其进行合理的近似就是一个关键。
拉普拉斯近似(Laplace Approximation)就是这样一种通过使用高斯分布来近似复杂分布的技术。显然它只能用于近似连续型分布。
核心思想
对于一个非负可积函数f ,记其积分为I(f):
I(f)=∫Xf(x)dx
拉普拉斯近似方法定义函数h(x) 如下:
h(x):=n1logf(x)
其中,h(x) 存在一个最值点x~,且有∇h(x~)=0。 将其在x=x~ 处泰勒展开到第三项:
h(x)=h(x~)+2!(x−x~)2∇2h(x~)+3!(x−x~)3∇3h(x~)+R3(x)
又由于ey=1+y+y2/2!+R3′。从而有:
I(f)=∫Xf(x)dx=∫Xenh(x)dx=∫Xenh(x~)e0.5n(x−x~)2∇2h(x~)en(x−x~)3∇3h(x~)/6dx≈enh(x~)∫Xe0.5n(x−x~)2∇2h(x~)[1+6n(x−x~)3∇3h(x~)+72n2(x−x~)3(∇3h(x~))2]dx
考虑一阶近似,我们可以得到:
I1(f)=enh(x~)∫Xe0.5n(x−x~)2∇2h(x~)dx
其中的被积函数正好是一个μ=x~,σ2=−1/n∇2h(x~) 的正态分布的密度函数。
由于使用到了二阶梯度,故得名为拉普拉斯近似。
多维版本
拉普拉斯近似方法 (Laplace Approximation) - 知乎 (zhihu.com)
局限性
根据推导不难得出 Laplace approximation 只能对单值函数f 进行近似。并且虽然可以通过增大近似阶数来增加近似程度,但是不可避免地需要计算复杂的 Hesse 矩阵,在计算机中的代价较大。
后验分布推导
贝叶斯推断之拉普拉斯近似 - 大熊猫同学 - 博客园 (cnblogs.com)
经典蒙特卡洛积分
经典蒙特卡洛积分 (Classical Monte Carlo integration)将积分式作如下变换:
I(f)=∫Xq(x)f(x)q(x)dx=Ex[q(x)f(x)]:=Ex[h(x)]
其中q(x) 是某个随机变量的 PDF.
根据辛钦大数定律,我们可以用一系列服从q(x) 的独立同分布 (independent and identically distributed, i.i.d.) 的样本{Xi}i=1m 的均值来近似此期望,即:
X
I(f)≈m1i=1∑mq(Xi)f(Xi):=μˉm
原始版本
相关性质
数值分析:数值积分(蒙特卡洛积分) - 知乎 (zhihu.com)
黎曼和估计法
对于一元函数来说,假设取X=[a,b] ,并取m+1 个点ai(i=1,2,...,m+1) 使得a=a1<a2<⋯<am+1=b 则当m→∞ 时,黎曼和趋近于积分值:
m→∞limi=1∑mf(ai)[ai+1−ai]=I(f)=∫abf(x)dx=∫abh(x)q(x)dx
其中h(x),q(x) 的定义与之前一致。
现在我们将确定点{ai}i=1m+1 更换为一组从q(x) 中抽取的 i.i.d. 的随机样本点,并排好序为{Xi}i=1m+1 ,则积分的估计值为:
I(f)≈i=1∑mf(Xi)[Xi+1−Xi]:=μR
这个值也被称为黎曼和估计(Riemannian sum estimator).
可以证明该方法在一元函数上的的收敛速度为O(m−2) 比经典蒙特卡洛积分方法的O(m−1) 更优。
重要性采样方法
加权估计
参考
- Inverse transform sampling - Wikipedia
- 用逆变换采样方法构建随机变量生成器 - MyEncyclopedia
- 【文献阅读 02】截断(truncated)正态分布 - 知乎
- 接受拒绝采样(Acceptance-Rejection Sampling) - 知乎
- Laplace Approximation-拉普拉斯近似 - 知乎
- 贝叶斯推断之拉普拉斯近似 - 大熊猫同学 - 博客园
- 拉普拉斯近似方法 (Laplace Approximation) - 知乎
- 数值分析:数值积分(蒙特卡洛积分) - 知乎
- 蒙特卡洛积分与重要性采样详解 - 烈日行者 - 博客园